exercise 10 :: Phonons calculation for silicon

The present exercise demonstrates calculation of phonons in harmonic approximation for silicon crystal, a non-polar material using Density Functional Perturbation Theory (DFPT). We will calculate phonons at Gamma point, discuss acoustic sum rule, and perform phonons calculation along high symmetry lines in Brillouin zone using Fourier interpolation.

TASK 01

Consider fcc Si crystal as discussed in exercise 7 and PBE pseudopotential (Si.pbe-n-kjpaw_psl.0.1.UPF) and perform scf calculations. For lattice constant assume 5.4310205 Angstrom and for Brillouin zone sampling 4x4x4 k-points. The input file for pw.x can read as:

&control
   title = 'Si with a=5.4310205 AA',
   calculation = 'scf'
   restart_mode='from_scratch',
   prefix='silicon',
   tstress = .true.
   tprnfor = .true.
   pseudo_dir = './',
   outdir='./tmp'
 /
&system
   ibrav = 2, celldm(1) = 10.26314155, nat = 2, ntyp = 1,
   ecutwfc = 38.0, ecutrho = 152,
 /
&electrons
   diagonalization='david'
   mixing_mode = 'plain'
   conv_thr =  1.0d-8
 /
ATOMIC_SPECIES
   Si  28.0855  Si.pbesol-n-kjpaw_psl.0.1.UPF
ATOMIC_POSITIONS alat
   Si  0.00  0.00  0.00
   Si  0.25  0.25  0.25
K_POINTS (automatic)
   4 4 4  0 0 0

TASK 02

Calculate phonons at Gamma point which can be performed using
ph.x -input ph_at_Gamma.in > out.ph_at_Gamma where the input file reads:

&inputph
  prefix='silicon',
  tr2_ph=1.0d-14
  amass(1)=28.0855,
  outdir='./tmp',
  fildyn='silicon.dyn'
/
0.0  0.0  0.0

When checking the dynamical matrix in silicon.dyn output file one sees that there are 6 modes, 3 acoustic and 3 optical. The vibrational Hamiltonian is invariant to a uniform spatial translation. This symmetry is the origin of the well-known result that any crystal has three acoustic vibrational modes at q = 0 with a frequency of zero. The so called acoustic sum rule of dynamical matrices should be zero

The calculated acoustic modes at Gamma point are degenerate but not equal to zero. Their values are 0.358751 THz, see below:

 Diagonalizing the dynamical matrix

 q = (    0.000000000   0.000000000   0.000000000 ) 

 **************************************************************************
    freq (    1) =       0.358751 [THz] =      11.966654 [cm-1]
 (  0.435633  0.000000  0.547320  0.000000 -0.103268  0.000000 ) 
 (  0.435633  0.000000  0.547320  0.000000 -0.103268  0.000000 ) 
    freq (    2) =       0.358751 [THz] =      11.966654 [cm-1]
 ( -0.055959  0.000000 -0.087431  0.000000 -0.699446  0.000000 ) 
 ( -0.055959  0.000000 -0.087431  0.000000 -0.699446  0.000000 ) 
    freq (    3) =       0.358751 [THz] =      11.966654 [cm-1]
 (  0.554159  0.000000 -0.439086  0.000000  0.010550  0.000000 ) 
 (  0.554159  0.000000 -0.439086  0.000000  0.010550  0.000000 ) 
     freq (    4) =      15.515850 [THz] =     517.553050 [cm-1]
 ( -0.347600  0.000000  0.325854  0.000000  0.522488  0.000000 ) 
 (  0.347600  0.000000 -0.325854  0.000000 -0.522488  0.000000 ) 
     freq (    5) =      15.515850 [THz] =     517.553050 [cm-1]
 (  0.381186  0.000000 -0.357339  0.000000  0.476452  0.000000 ) 
 ( -0.381186  0.000000  0.357339  0.000000 -0.476452  0.000000 ) 
     freq (    6) =      15.515850 [THz] =     517.553050 [cm-1]
 ( -0.483603  0.000000 -0.515876  0.000000  0.000000  0.000000 ) 
 (  0.483603  0.000000  0.515876  0.000000 -0.000000  0.000000 ) 
 **************************************************************************

This is a consequence of perturbative approach. To correct dynamical matrix run dynmat.x -i dynmat.in where the dynmat.in file should read:

&input
 fildyn='silicon.dyn',
 asr='simple'
/

Inspect the acoustic modes frequencies after the correction.

TASK 03

Calculate phonon dispersion along the W-X-$\Gamma$-L-K path in the first Brillouin zone.

1. Perform phonon calculation on regular 4x4x4 q-gridu using ph.x with the following input:

   &inputph
    prefix='silicon',
    tr2_ph=1.0d-14
    amass(1)=28.0855,
    ldisp=.true.,
    nq1=4,
    nq2=4,
    nq3=4,
    outdir='./tmp',
    fildyn='silicon.dyn'
   /
   

2. Calculate interatomic force constant using q2r.x program using the input:

    &input
     fildyn='silicon.dyn'
     zasr='simple'
     flfrc='silicon_nq444.fc'
    /
   

3. Calculate phonons at generic q-point, e.g., along the W-X-$\Gamma$-L-K path use the matdyn.x -i matdyn.in > out.matdyn where the input file can be downloaded here. The file contains 142 q-points in crystal units (the first three columns) that can be generated using, e.g., pw.x program with calculation = 'bands' and setting verbosity = 'high'

    K_POINTS crystal_b
    5
       0.75  0.50  0.25   21
       0.50  0.50  0.00   60
       0.0   0.0   0.0    51
       0.50  0.50  0.50   9
       0.75  0.375 0.375  1
   

   The point coordinates can be get using xcrysden
   
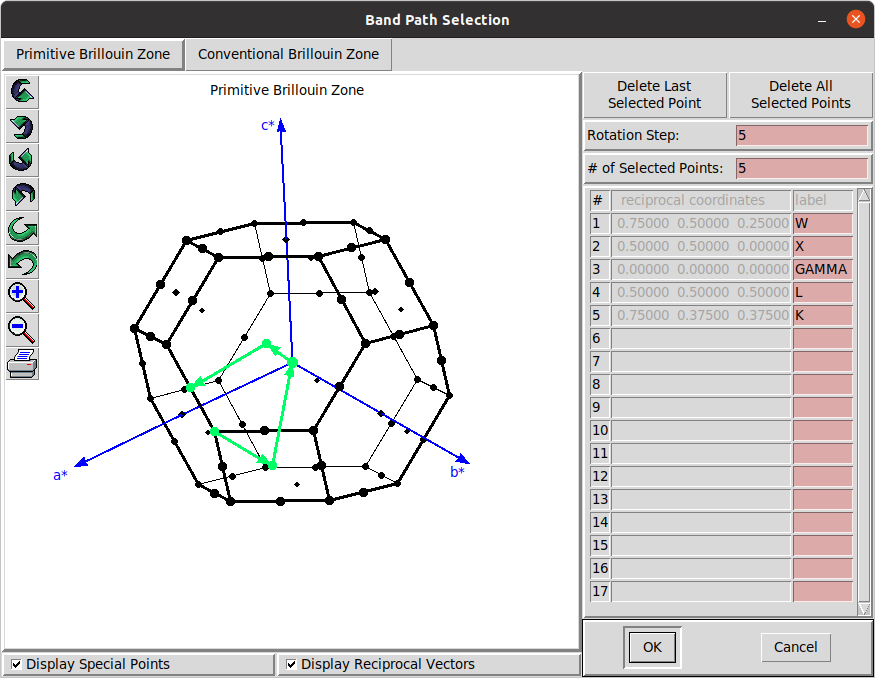
   The forth column is the q-path length that can be obtained from the output file for gnuplot bandstructre plotting generated by bands.x.

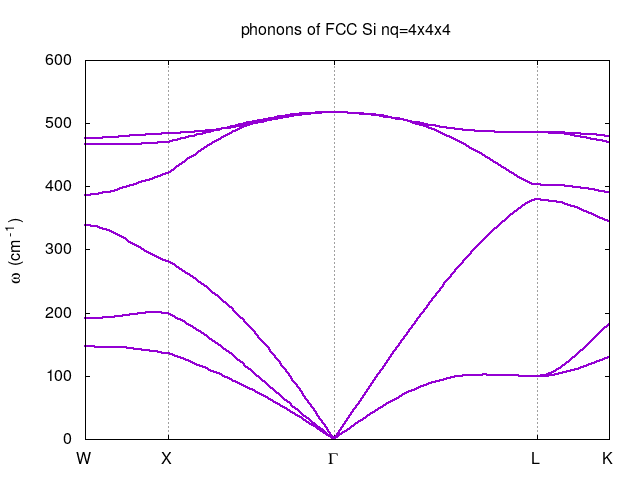
4. Finally the phonon dispersion can be plot by gnuplot as

    set term x11
    set title "phonons of FCC Si nq=4x4x4"
    set grid xtics
    set xtics ("W" 0, "X" 0.353553, "{/Symbol G}" 1.060660, "L" 1.926686, "K" 2.232872)
    set ylabel "{/Symbol w} (cm^{-1})"
    plot for [col=2:7] 'silicon.freq.gp' u 1:col t"" with lines lt 1
   

Martin Gmitra :: martin.gmitra@upjs.sk
This work is licensed under a Creative Commons Attribution 4.0 International License.