exercise 08 :: Calculation of magnetic properties of bcc Fe and FeO

The present exercise aims to demonstrate the self-consistent field calculations for cubic bulk bcc Fe and FeO crystals. We demonstrate calculation od spin polarized band structure and density of states, as well as inclusion of Hubbard U correction to on-site energy important for treating correlation effects in d-shell for FeO.

TASK 01

Consider bcc Fe with lattice constant of 2.856 Angstrom and perform self-consistent field calculations for non-magnetic case. The input file could look like

&control
   calculation = 'scf'
   restart_mode = 'from_scratch'
   prefix = 'Fe_NM'
   pseudo_dir = './'
   outdir = './tmp'
 /
&system
   ibrav = 3, celldm(1) = 5.3970579, nat = 1, ntyp = 1
   ecutwfc = 64, ecutrho = 782
   occupations = 'smearing', smearing = 'marzari-vanderbilt', 	degauss = 0.05
 /
&electrons
   diagonalization = 'david'
   conv_thr = 1.0e-8
   mixing_beta = 0.6
 /
ATOMIC_SPECIES
	Fe  55.847  Fe.pbe-spn-kjpaw_psl.0.2.1.UPF
ATOMIC_POSITIONS alat
	Fe  0.0  0.0  0.0
K_POINTS automatic
    8 8 8  0 0 0

To perform self-consistent field calculations of ferromagnetic phase one sets up the following variables to &system block

    nspin = 2
    starting_magnetization(1) = 1.5

in which you instruct the code to perform spin-polarized calculations with starting magnetization on first atom in the ATOMIC_SPECIES list.
Remember also to change prefix in case you would like to use converged electronic density of ferromagnetic case for further postprocessing.

Consider now antiferromagnetic order of magnetic moments on the neighboring Fe atoms and perform self-consistent field calculation of the total electronic energy. Hint: for the calculation you need to modify the structure considering a cubic primitive cell and two non equivalent Fe atoms and setting the starting magnetization in opposite directions.

Compare your results for the total electronic energies with the following table and discuss the magnetic ground state.

bcc Fe	non-magnetic	ferromagnetic	antiferromagnetic
total energy per atom (Ry)	-329.2312	-329.2596	-329.2343

Consult results for total magnetization and absolute magnetization values for the magnetic cases. The ferromagnetic phase is the ground state with magnetic moment per Fe atom of 2.14 $mu_B$ with good agreement with experimental value 2.22 $mu_B$ .

Exchange integral from total energy

The exchange integral can be determined by mapping the DFT results to the Heisenberg spin model Hamiltonian meaning we require that the total energies are equal. The Hamiltonian in this case reads
$enter image description here$
where $enter image description here$ is the exchange integral and $enter image description here$ is the spin angular momentum operator at site i.

Assuming the nearest neighbors, in our case each Fe atom has the 8 neighbours, and the energy of the ferromagnetic state is then $E_FM$ and for antiferromagnetic state $E_AFM$ . The exchange integral is equal $enter image description here$ . The Curie temperature within the mean ﬁeld approximation is
$enter image description here$
which for the bcc Fe leads to $enter image description here$ overestimating experimental value.

TASK 02

Calculate density of states (DOS), projected density of states (PDOS) considering Fe d-orbitals and band structure for ferromagnetic ground state of bcc Fe.

To calculate DOS and PDOS one needs to perform calculation = 'nscf' with larger k-point Brillouin zone sampling. Consider k-point sampling with 12x12x12 and tetrahedron method setting occupations = 'tetrahedra' similar inputs we prepared in exercise 05.

For total DOS calculations using dos.x we consider the following input

	&DOS
	   prefix = 'Fe_FM'
	   outdir = './tmp'
	   bz_sum = 'tetrahedra'
	   emin = 8.0
	   emax = 33.0
	   deltaE = 0.1
	   fildos = 'tetra_de0.1.dos'
	/

and for PDOS using projwfc.x program

	&projwfc
	    prefix = 'Fe_FM',
	    outdir = './tmp'
	    filproj = 'pdos.proj'
	    emin = 8
	    emax = 33
	/

To calculate band structure calculation = 'bands' along the high symmetry lines connecting $k-path$ (for the point coordinates see Sec. 1.3 in W. Setyawan and S. Curtarolo)
use:

K_POINTS crystal_b
6
0.0 0.0 0.0 		34	G
0.5 0.5 0.5 		28	H
0.5 0.0 0.0 		17	N
0.25 -0.25 0.25 	17	P
0.0 0.0 0.0  		20	G
0.5 0.0 0.0 		1	N

The bands.x program should be run afterwards separately for spin up and spin down specifying spin_component = 1 and spin_component = 2 in the input:

 &bands
    prefix  = 'Fe_FM'
    outdir = './tmp'
    filband = 'bands_up.dat'
    spin_component = ?
    lsym = .false.
 /

To plot the results you can use the following gnuplot script

set term x11
set multiplot layout 1,2 title "Bandstructure and DOS of BCC Fe"
#BANDS subfigure
EF=17.6895645097 #taken from tetra_de0.1.dos file

set grid xtics
set xtics ("{/Symbol G}" 0, "H" 1.0, "N" 1.7071067812, "P" 2.2071067812, "{/Symbol G}" 3.0731321850, "N" 3.7802389662) out nomirror offset 0,0.25
set ytics out nomirror offset 0.75,0

set xlabel " "
set ylabel "E - E_F (eV)" offset 1,0

set linestyle 1 lc rgb "#aa0000" lt 1 lw 2
set linestyle 2 lc rgb "#0000aa" lt 1 lw 2

p [:][-10:15] \
'bands_up.dat.gnu' u 1:($2-EF) t"" w l ls 1, 'bands_dn.dat.gnu' u 1:($2-EF) t"" w l ls 2 ,\
 0 t"" lw 0.1 lt 6

#DOS subfigure
set xtics auto
unset ylabel
set xlabel "DOS (1/eV)"
set style fill noborder
set style fill transparent solid 0.35 noborder

set key right spacing 1.25 font "Helvetica,10"
unset grid

set linestyle 3 lc rgb "#008800" lt 1 lw 2
set linestyle 4 lc rgb "#112200" lt 1 lw 2

p [-3:3][-10:15] \
  'tetra_de0.1.dos' u ($2):($1-EF) t"up" w l ls 1, '' u (-$3):($1-EF) t"dn" w l ls 2,\
  'Fe_FM.pdos_atm#1(Fe)_wfc#5(d)' u 4:($1-EF) t"d_{z^2}" w filledcurves ls 3, '' u (-$5):($1-EF) t"" w filledcurves ls 3,\
  '' u 12:($1-EF) t"d_{xy}" w filledcurves ls 4, '' u (-$13):($1-EF) t"" w filledcurves ls 4,\
  0 t"" lw 0.1 lt 6

unset multiplot

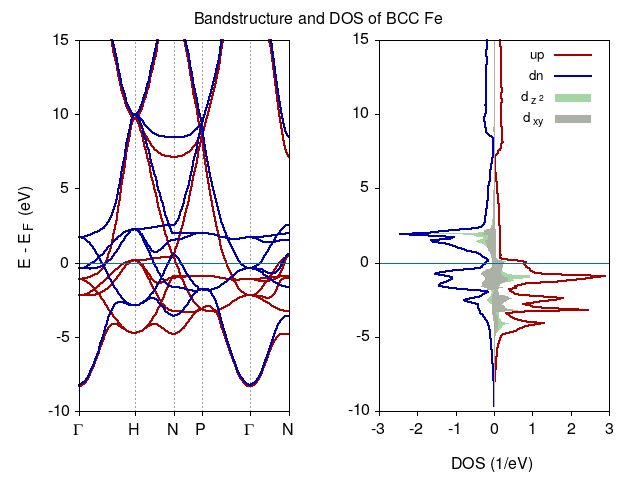
bcc Fe bands and pdos

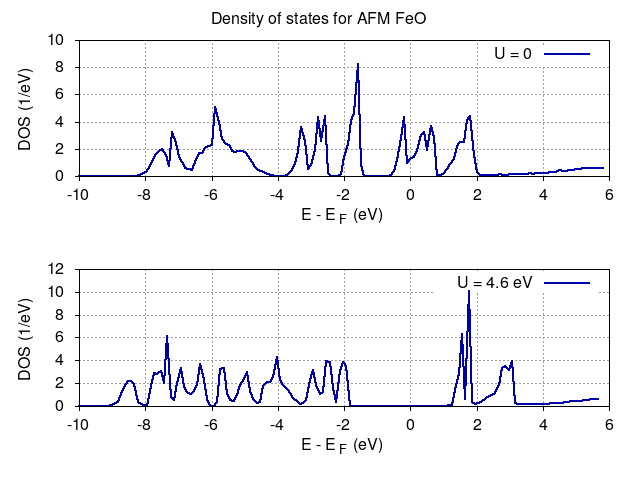
TASK 03

Calculate DOS for antiferromagnetic rock-salt cubic crystal FeO and compare results with on-site Hubbard potential U=4.6 eV for d electrons of Fe.
The input for the self-consistent field calculations reads as follows:

&control
    calculation='scf'
    restart_mode='from_scratch',
    prefix='FeO'
    pseudo_dir = './'
    outdir='./tmp/'
    verbosity='high'
 /
 &system
    ibrav = 0,
    celldm(1) = 8.19,
    nat = 4, ntyp = 3,
    ecutwfc = 40, ecutrho = 460,
    occupations = 'smearing', smearing = 'mv', degauss = 0.02,
    nspin = 2,
    starting_magnetization(1) =  0.5,
    starting_magnetization(2) = -0.5
    lda_plus_u = .true.,
    lda_plus_u_kind = 0,
    U_projection_type = 'atomic',
    Hubbard_U(1) = 4.6
    Hubbard_U(2) = 4.6
    starting_ns_eigenvalue(1,1,1) = 1.2d0
    starting_ns_eigenvalue(2,1,1) = 1.2d0
    starting_ns_eigenvalue(3,1,1) = 0.d0
    starting_ns_eigenvalue(4,1,1) = 1.2d0
    starting_ns_eigenvalue(5,1,1) = 0.d0
    starting_ns_eigenvalue(1,2,2) = 1.2d0
    starting_ns_eigenvalue(2,2,2) = 1.2d0
    starting_ns_eigenvalue(3,2,2) = 0.d0
    starting_ns_eigenvalue(4,2,2) = 1.2d0
    starting_ns_eigenvalue(5,2,2) = 0.d0
    nbnd = 50
 /
 &electrons
    conv_thr =  1.d-9
    mixing_beta = 0.3
    mixing_fixed_ns = 8
 /
ATOMIC_SPECIES
    Fe1  55.845  Fe.pbe-spn-kjpaw_psl.0.2.1.UPF
    Fe2  55.845  Fe.pbe-spn-kjpaw_psl.0.2.1.UPF
    O     16.0   O.pbe-n-kjpaw_psl.1.0.0.UPF
CELL_PARAMETERS {alat}
    0.50  0.50  1.00
    0.50  1.00  0.50
    1.00  0.50  0.50
ATOMIC_POSITIONS {crystal}
    Fe1  0.00  0.00  0.00
    Fe2  0.50  0.50  0.50
    O    0.25  0.25  0.25
    O    0.75  0.75  0.75
K_POINTS {automatic}
    3 3 3 0 0 0

Density of states for U=0 and U=4.6 eV are shown below demonstrates spectral gap opening and change from metallic to insulating phase in accordance with experiment.

enter image description here

Martin Gmitra :: martin.gmitra@upjs.sk
This work is licensed under a Creative Commons Attribution 4.0 International License.